Generate and plot some data from a line.
set.seed(313)
n = 100
x = seq(0, 1, length.out = n)
y = 2 * x + 1 + rnorm(n) * 0.5
plot(x, y, main = paste0("Sample correlation: ", round(cor(x,y), 3)))
abline(lm(y ~ x))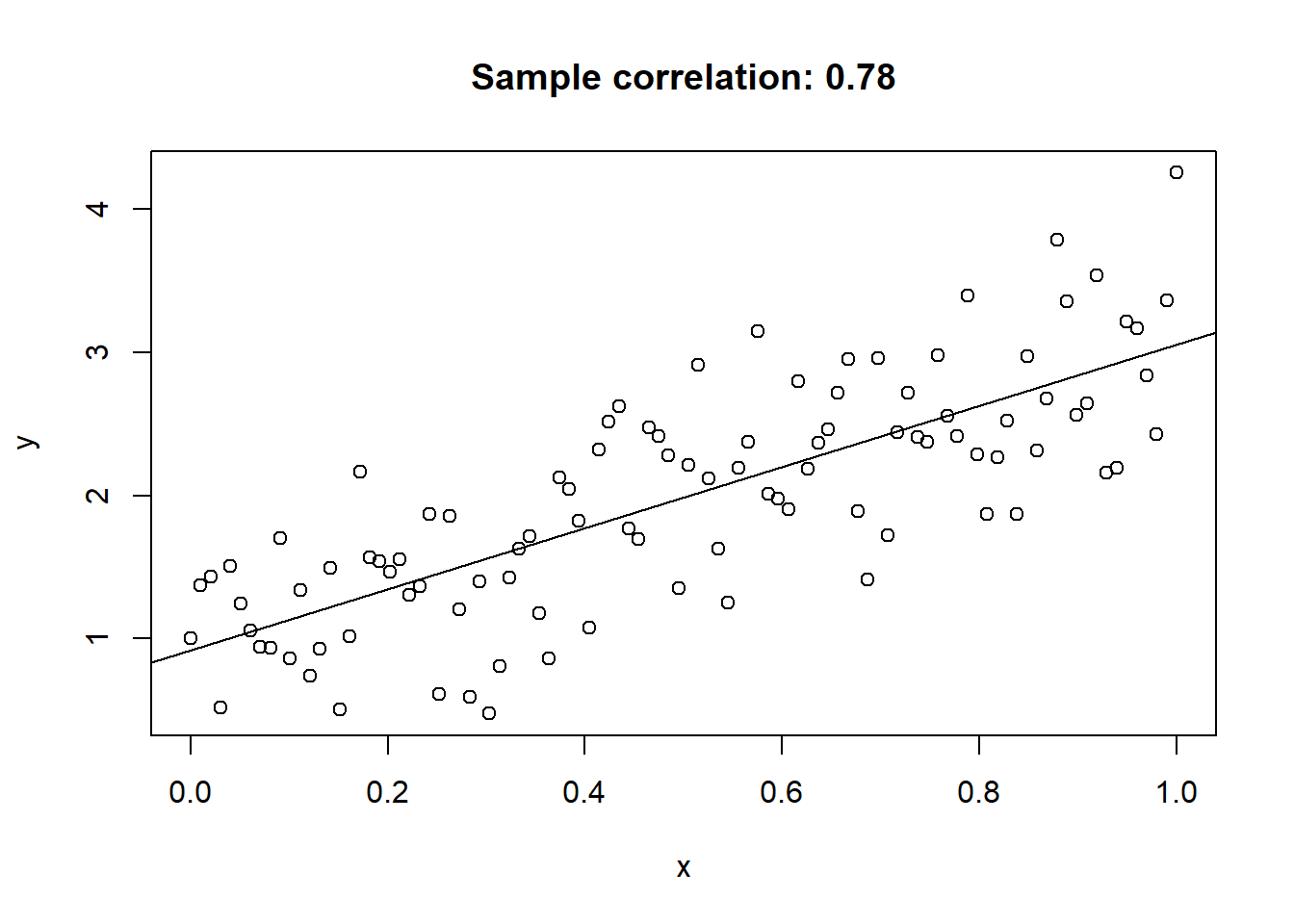
Jonas Moss
Jan 25, 2023
What is this? A rant about an unimportant problem. Read at your own risk!
Everyone knows the correlation coefficient. It measures the degree of linear dependence between two random variables

That should be familiar. But what if there are TWO parallel lines in the data?!
set.seed(313)
par(mfrow=c(1,2))
n = 50
x1 = seq(0, 1, length.out = n)
y1 = 2 * x1 + 1 + rnorm(n) * 0.5
x2 = seq(0, 1, length.out = n)
y2 = 2 * x2 + 2 + rnorm(n) * 0.5
plot(x1, y1, main = paste0("Sample correlation: ???"), col = "blue", ylim = c(0, 6), xlab = "x", ylab = "y")
points(x2, y2, col = "red")
abline(a = 1, b = 2, col = "blue")
abline(a = 2, b = 2, col = "red")
x = c(x1, x2)
y = c(y1, y2)
z = c(rep(0, 50), rep(1, 50))
plot(x, y, main = paste0("Sample correlation: ", round(cor(x,y), 3)), xlab = "x", ylab = "y", ylim = c(0, 6))
abline(a = 3/2, b = 2)
abline(a = 1, b = 2, lty = 2)
abline(a = 2, b = 2, lty = 2)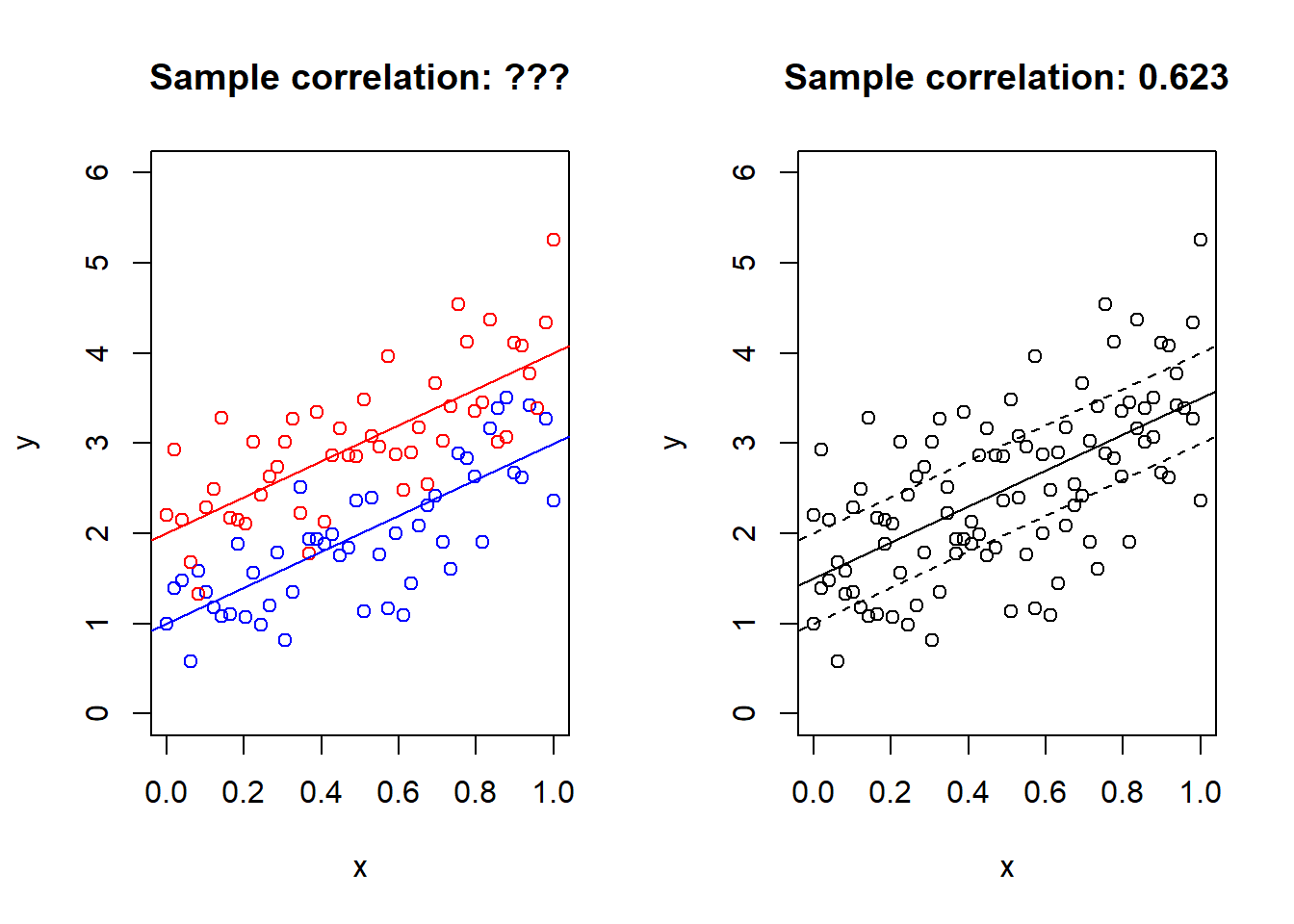
The data has been simulated from the model
If we know the joint distribution of
Calculating this correlation coefficient is easy as pie.
And its much larger than the “one-line correlation”, going from
So, we know the joint distribution of
I can’t think of an efficient way to calculate upper bounds, but the lower bound is simple enough (in the case when the correlation is positive): It equals z)and fit the regression model y ~ x + z. But that would be
However, consider the following data
Since
n <- 15
x <- mtcars$drat[1:n]
y <- mtcars$wt[1:n]
n <- length(x)
mat <- cbind(1, x, 0)
minimum = Inf
for(k in seq(0:n)) {
icomb <- arrangements::icombinations(n, k)
choose(n, k)
for(i in seq(choose(n, k))) {
indices <- icomb$getnext()
mat[, 3] <- 0
mat[indices, 3] <- 1
mod <- lm.fit(mat, y)
current <- sum(mod$residuals^2)
if (current < minimum) {
minimum = current
z = indices
coef <- mod$coefficients
}
}
}
cor2 <- sqrt(1 - minimum/sum((y - mean(y))^2)) * sign(coef[2])
cor1 <- cor(x, y)From the code above we find that lower and upper bounds for the two lines correlation:
Let’s also have a look at the classification of points that maximizes this correlation.
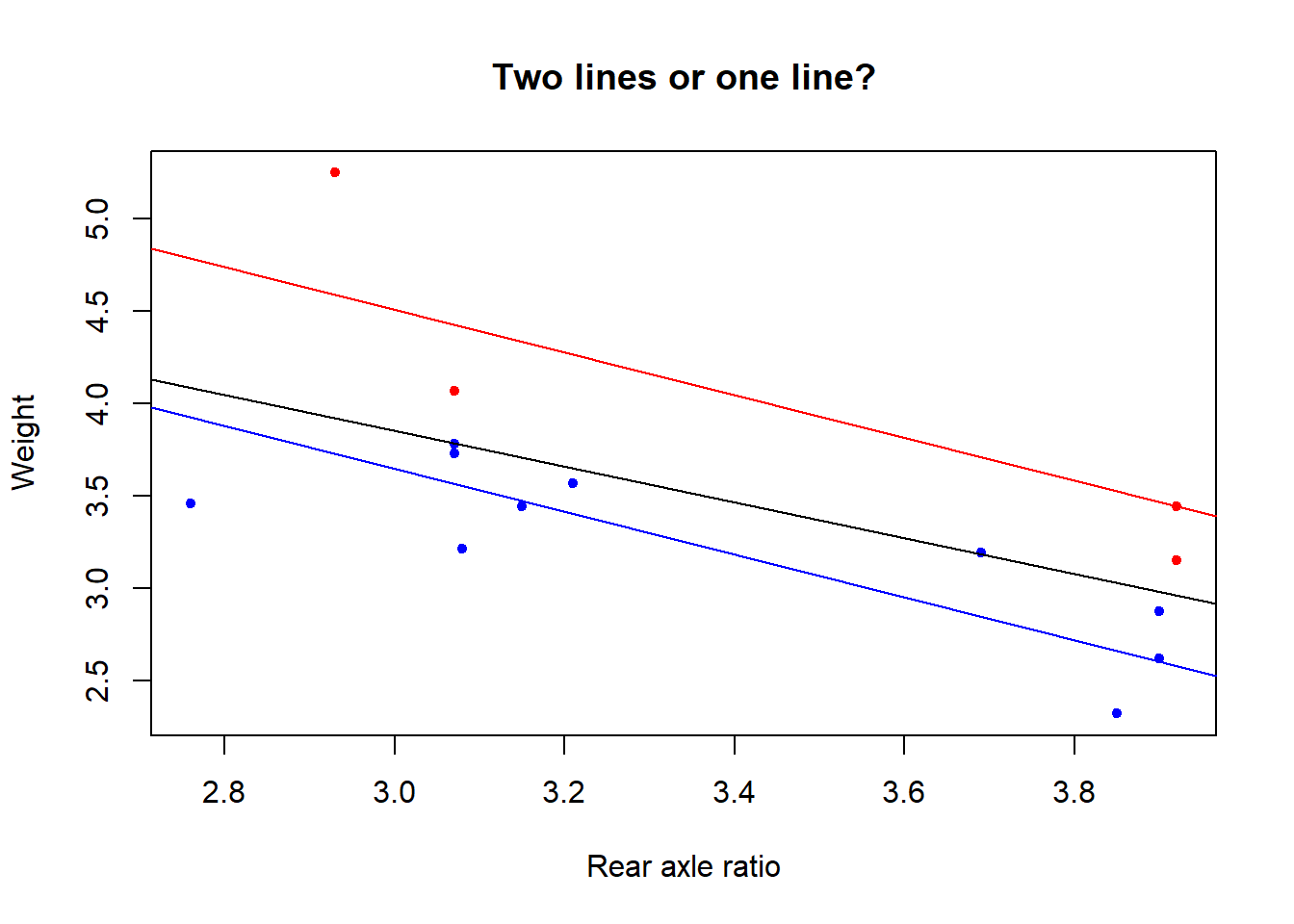
The two lines correlation for this optimal classification equals the lower bound above.